Something / Nothing
somethingnothing.net is an interactive film clip for the track "Something / Nothing" by Alpha Beta Fox. It was created with JavaScript and uses the WebGL (via three.js) and Web Audio HTML 5 APIs.
WebGL is a JavaScript API for rendering interactive 2D and 3D graphics within any WebGL compatible web browser without the use of plug-ins.
The Web Audio API is a JavaScript API for processing and synthesizing audio within Web Audio API compatible web browsers.
three.js is a JavaScript Library which makes using WebGL simpler.
Alpha Beta Fox
Alpha Beta Fox are a band from Adelaide, Australia.
Its members are: Gordo, Tanya, Nic, Jon, Bec
Members: Gordo, Tanya, Nic, Jon, Bec
The five-piece pull together the best parts of Lush, St Etienne and brighter moments of mid-'80s The Cure. Alpha Beta Fox boast the dual vocal talents of Tanya Giobbi and Rebecca Burge Versteegh and, of course, churning, chiming guitars. Far from being copyists however, ABF also use Theremin, inspired fizzing synth and a bird whistle to create their genuinely unusual sound. Opening song Lady Don't Ride instantly announces them as one of the boldest and brightest discoveries so far this year
More Alpha Beta Fox: Facebook SoundCloud Spotify iTunes
You can watch a video below of Alpha Beta Fox at the Grace Emily filmed by Spoz:
The Fox Model
The fox model is from the Open Source interactive film 3 Dreams of Black. The code and the assets for the film can be downloaded from the 3 Dreams of Black Tech Page.
The model was produced by Mirada Studios, a "multiplatform storytelling company" formed by Guillermo del Toro, Mathew Cullen, Guillermo Navarro, and Javier Jimenez.
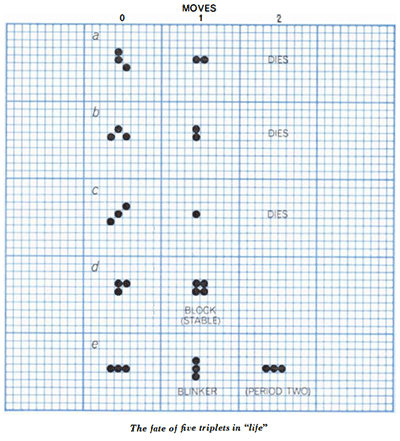
Conway's Game of Life
The Game of Life is a cellular automaton devised by the British mathematician John Conway in 1970. A digital issue of Scientific American containing the "Mathematical Games" article describing the Game of Life can be purchased from the Scientific American website: Scientific American Magazine, October 1970 Issue. The article can also be read on archive.org: The fantastic combinations of John Conway's new solitaire game "life".
In Conway's Game of Life, whether a cell is born, lives or dies is determined by its current state and the state of its neighbouring 8 cells:
- Survivals. Each live cell with two or three neighboring counters survives for the next generation.
- Deaths. Each cell with four or more neighbors dies from overpopulation. Every cell with one neighbor or none dies from isolation.
- Births. Each empty cell adjacent to exactly three neighbors--no more, no fewer--is a birth cell. A counter is placed on it at the next move.
You can watch a video below of John Conway talking about the creation of the Game of Life:
The Spaceship Model
The Spaceship model was created by Françs "CoyHot" Grassardd and released under the Creative Commons Attribution 3.0 Unported licence. The licence allows anyone to freely share or adapt the model as long as appropriate credit is given.
The model can be downloaded from Blend Swap: Small Spaceship.
The Landscape
The landscape was originally intended to be based on videos by Beeple. Beeple releases video loops and the Cinema 4D projects used to make the videos under the Cretive Commons license. Beeple's videos can be seen on his Beeple Vimeo channel.
In the end, the landscape doesn't look much like Beeple, but still contains some Beeple elements, such as the cicles and crosses.
OpenGL Shading Language (GLSL)
GLSL is a high level programming language which can be used to create short programs, called shaders, to be executed on a computer's graphics processing unit.
This website uses pixel shaders which are modifications of shaders found in the GLSL Sandbox Gallery. Pixel shaders calculate the colour of a pixel based on data passed to them. The Shadertoy website also contains many shaders.
Try out some pixel shaders:
The Tesseract
A tesseract is the four dimensional analog of the cube. Being a four dimensional object, a tesseract can be difficult to visualise. A projection of a tesseract into three dimensional space can be formed by connecting the corresponding corners of two cubes. This is analagous to projecting a cube into two dimensional space by drawing two squares and connecting their corners.
You can watch Carl Sagan attempt to explain Tesseracts and 4 dimensional space using apples in the video below:
The Kali Set
The Kali Set is a simple algorithm created by Fractal Forums user "Kali" for creating fractal patterns. The thread on fractal forums can be viewed here: Very simple formula for fractal patterns.
A fractal is a natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. So a zoomed in fractal will look similar to a zoomed out version of the same fractal. Although the history of the fractal goes back to the 17th century, Benoit Mandelbrot coined the term "fractal" in 1975. In the below video you can watch Benoit Mandelbrot give a TED talk on "Fractals and the art of roughness":
Hopalong Orbits
Hopalong orbits were discovered by Barry Martin from Aston University in England. A.K. Dewdney presented the Hopalongs in his "Computer Recreations" column of the September 1986 Issue of Scientific American Magazine. Barry Martin commented in the magazine: "It seems to me we are on the verge of a pattern-generating explosion that has great commercial implications, e .g ., we can expect to see 'designer' wallpaper and textiles within the next few years. Patterns will be produced by the customer merely by the selection of a few numbers."
In a Hopalong orbit, the location of each point is determined by inputting the location of the previous point into a simple formula. This is where the name "hopalong" comes from, as points will hop along elliptical orbits. Colours are determined by the number of interations it takes to get to a point.
Variations of Barry Martin's original Hopalong orbits have been produced since 1986. This website uses the following four:
-
Hopalong:
xn + 1 = yn - sgn(xn)*sqrt|b*xn - c|
yn + 1 = a - xn
-
Martin:
xn + 1 = yn - sin(xn)
yn + 1 = a - xn
-
Three Ply:
xn + 1 = yn - sgn(xn)|sin(xn)cos(b) + c - xnsin(a + b + c)|
yn + 1 = a - xn
-
Quadrup Two:
xn + 1 = yn - sgn(xn) * sin(ln|b * xn - c|) * atan(|c * xn - b|2)
yn + 1 = a - xn
sgn() will return negative one if its argument is negative and positive one if its argument is positive
The code used to implement these orbits is based on Iacopo Sassarini's Barry Martin's Hopalong Orbits Visualizer. In addition to colouring subsets of points differently, Iaco Sassarini seperates them in space along the z-axis (the axis going into the screen)
You can try out some Hopalong orbits using the controls below:
Easter Eggs
There are some easter eggs within the clip. Most can be found with use of the mouse. Try clicking on stuff, or holding down the button and dragging. The mouse can also be used in the banner in most sections of this page.